SARIMA Forecasting

A Simple Guide to SARIMA Forecasting

What is Time Series Forecasting?

Time series forecasting is a technique used to predict future values based on previously observed values. In time series data, observations are collected over time—usually at regular intervals (e.g., daily, monthly, yearly).

For example, a police department might track the number of reported crimes each month. By analysing past crime data, they can forecast future trends, helping them allocate resources more effectively and improve public safety.

What is SARIMA?

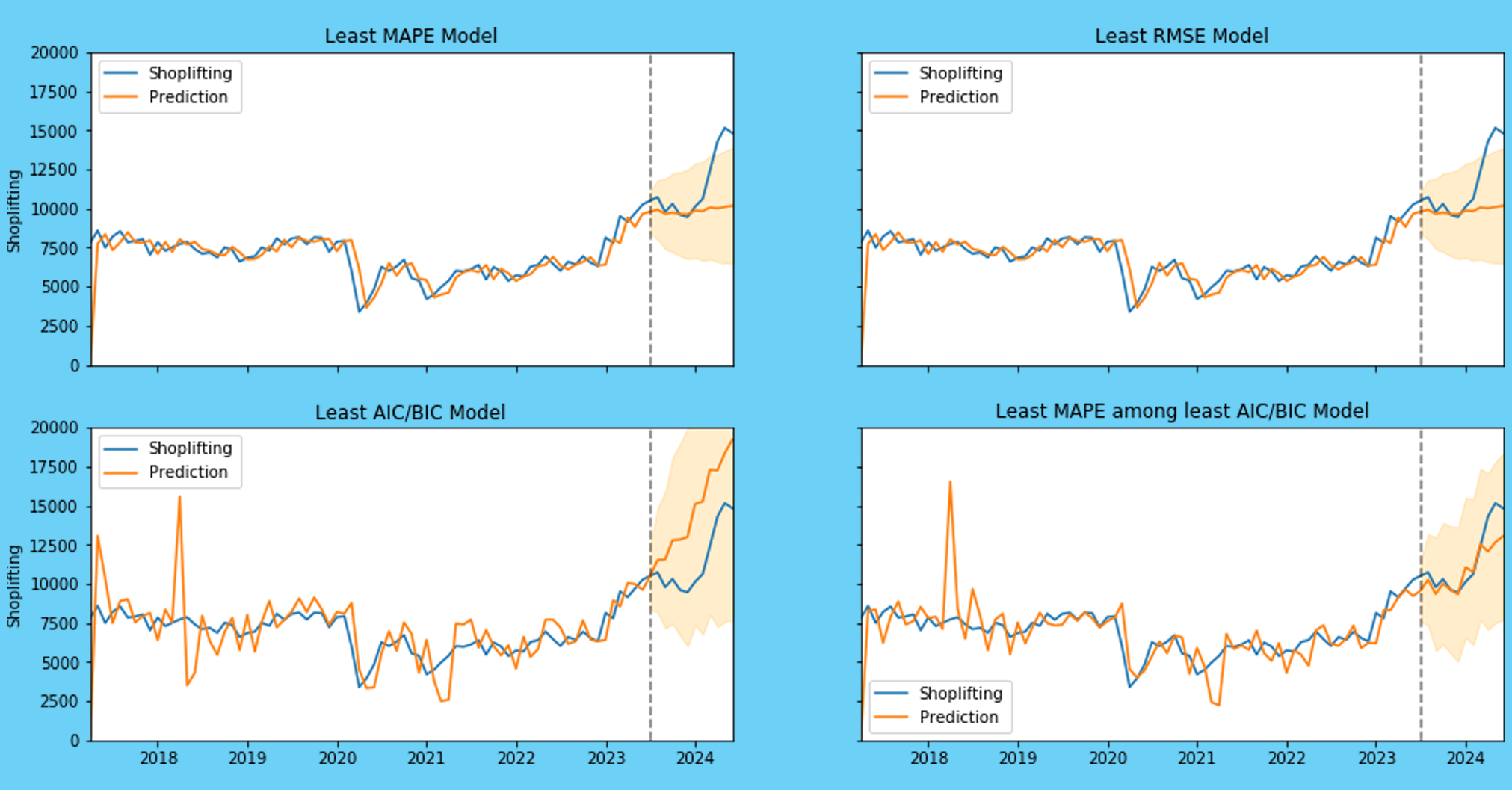
SARIMA, which stands for Seasonal Autoregressive Integrated Moving Average, is an advanced statistical method used for time series forecasting. It extends the basic ARIMA model by adding seasonal components, making it particularly useful for data with seasonal patterns.

ARIMA vs. SARIMA

• ARIMA: A model that focuses on capturing non-seasonal trends in time series data.
• SARIMA: An extension that incorporates both non-seasonal and seasonal effects, allowing for better forecasts in cases where the data has periodic fluctuations (like increased crime rates during holidays).

Why/When to Use SARIMA?

SARIMA is ideal for forecasting time series data that exhibit:

• Seasonality: Regular patterns that repeat over time. For instance, certain crimes may spike during specific seasons or holidays, like increased thefts during the holiday shopping season.
• Trends: Long-term upward or downward movements in data. For example, a gradual increase in overall crime rates over several years may warrant the use of SARIMA to understand and predict future occurrences.

Using SARIMA can help organisations like police departments to:

• Better prepare for expected increases in crime during certain times of the year.
• Evaluate the effectiveness of interventions over time by comparing actual crime rates against forecasts.

Components of SARIMA

SARIMA consists of several key components, typically represented as 𝑆𝐴𝑅𝐼𝑀𝐴(𝑝,𝑑,𝑞)(𝑃,𝐷,𝑄,𝑠):

• p: The number of autoregressive (AR) terms. This captures the influence of past values on the current value.
• d: The number of differences needed to make the series stationary (i.e., the mean and variance are constant over time).
• q: The number of moving average (MA) terms. This captures the influence of past forecast errors on the current value.
• P: The number of seasonal autoregressive terms.
• D: The number of seasonal differences.
• Q: The number of seasonal moving average terms.
• s: The length of the seasonal cycle (e.g., s = 12 for monthly data that has annual seasonality).

Example

Consider a city police department analysing monthly burglary reports. If they observe that burglaries tend to increase during the summer months and decrease during winter, SARIMA can be applied to model this seasonal pattern:

• p: Use past burglary data to see how previous months’ counts affect the current month’s count.
• d: Determine how many times the data needs to be differenced to stabilise the mean.
• q: Incorporate previous errors in the forecasts into the current prediction.
• P, D, Q, s: Model the seasonal patterns observed during summer months (e.g., higher burglaries in June, July, and August).

Strengths and Limitations of SARIMA

Strengths:

• Handles Seasonality: SARIMA is specifically designed to model data with seasonal patterns, making it effective for many real-world applications.
• Flexible: It can capture various patterns in data, including trends and seasonal fluctuations.
• Widely Used: SARIMA is a well-established method in statistical forecasting, with robust theoretical foundations and practical applications.

Limitations:

• Complexity: Determining the optimal values for p, d, q, P, D, Q, and s can be complex and time-consuming, requiring expertise and careful analysis.
• Assumes Stationarity: While SARIMA can handle trends and seasonality, the underlying data must be stationary, meaning it has consistent mean and variance over time. This may require additional preprocessing steps.
• Sensitivity to Outliers: SARIMA can be sensitive to outliers in the data, which can skew predictions if not addressed.

Summary

SARIMA forecasting is a powerful tool for time series analysis, especially when dealing with seasonal data, such as crime statistics. By understanding the components and strengths of SARIMA, decision-makers can better utilise this method to anticipate future trends and make informed decisions in resource allocation and crime prevention strategies.

Key Takeaways

• SARIMA forecasting is a powerful tool for analysing and predicting time series data with trends and seasonal patterns.
• SARIMA consists of several components: AR, I, MA, and S, which work together to model complex data behaviors.
• This method is particularly useful in the crime domain for forecasting crime trends, aiding in resource allocation, and strategic planning.

Glossary of Key Terms

• Time Series Data: Data collected at consistent intervals over time.
• Stationary Data: Data that has a constant mean and variance over time.
• Differencing: The process of subtracting an observation from a previous observation to eliminate trends.
• Lag Observations: Past values of the time series used to predict future values.
• Seasonality: Regular patterns that repeat at fixed intervals, such as monthly or yearly fluctuations.