Logistic Regression

Logistic Regression

What is Logistic Regression?

Logistic regression is a statistical method used to predict the probability of a binary outcome (i.e., an outcome with two possible values, such as “yes” or “no”, “success” or “failure”, “crime” or “no crime”). Unlike linear regression, which predicts a continuous outcome, logistic regression is used when the outcome is categorical.

Simple Example

Imagine you want to predict if a person will reoffend based on their background and behavior while in prison. Logistic regression can help you calculate the probability of reoffending. Instead of predicting exact numbers, logistic regression gives us a probability, like the chance that a person with certain risk factors will reoffend after release.

The chart below shows that as the the number of prior offences increases as well as the age of the offender the likelihood of reoffending increases – shown by the decision boundaries.

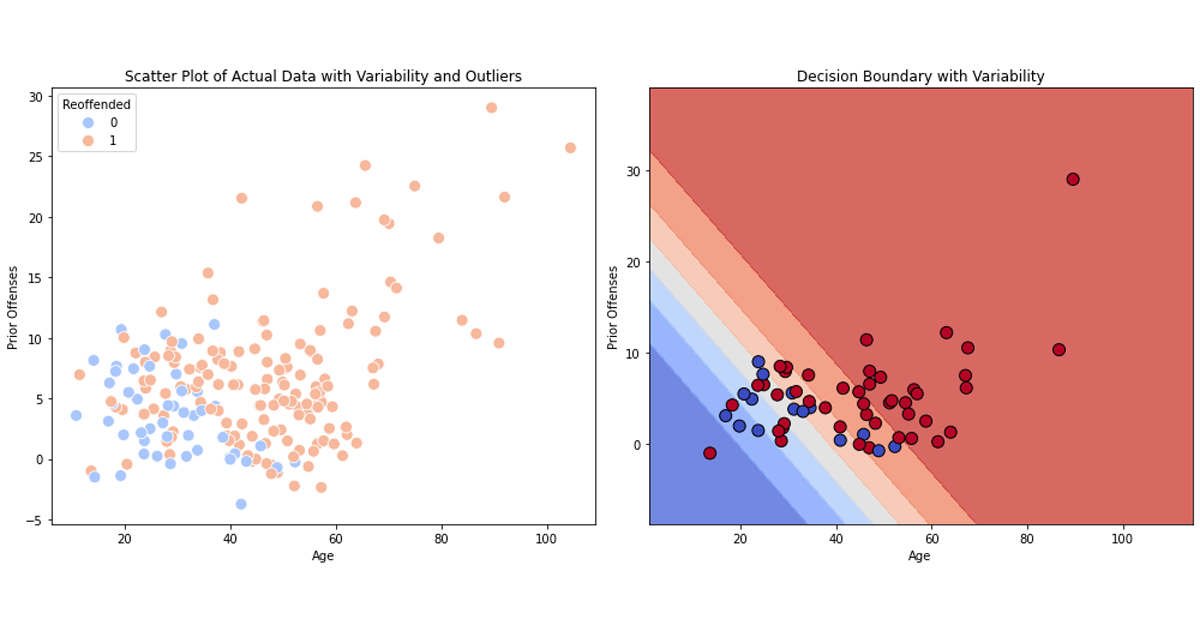Plot Showing the Results of a Logistic Regression on Reoffending Likelihood

How Does Logistic Regression Work?

Logistic regression evaluates different factors (such as previous offences, age, and behavior in prison) to estimate the probability of a specific outcome (like reoffending). It uses a special function to ensure that this probability is always between 0 and 1. If the probability is greater than 0.5, the outcome is likely to happen; if it’s less than 0.5, it’s less likely. For example, if the model predicts a 70% chance of reoffending, it suggests a likelihood of reoffending.

When Should You Use Logistic Regression?

Use logistic regression when:

• You need to predict a binary outcome, such as whether a person will reoffend or not.
• You want to understand how different factors impact the probability of an event occurring. For example, logistic regression can show how factors like prior criminal history affect the likelihood of recidivism.

What Can Logistic Regression Tell Us?

Logistic regression provides:

• Probabilities: It estimates how likely an event is to occur. For example, it might predict there is an 80% chance that a person with certain characteristics will reoffend.
• Impact of Factors: It shows how different factors affect the likelihood of the outcome. For example, it can reveal how previous offenses or age increase the probability of reoffending.

Practical Use of Logistic Regression

Logistic regression is valuable for:

• Predicting Outcomes: Estimating the likelihood of a specific event occurring based on different factors. For example, it can predict whether an individual will take a certain action or experience a particular event
• Assessing Risk Factors: Identifying which factors are most strongly associated with an increased or decreased probability of the outcome. For instance, it can help determine how certain variables, such as previous history or personal characteristics, impact the likelihood of an event happening.

What Logistic Regression Can’t Do

Logistic regression is limited by:

• More Than Two Outcomes: It is suited for predicting binary outcomes (e.g., reoffending/no reoffending). For cases with multiple categories, other methods are needed.
• Complex Relationships: It might not capture very complex relationships. For example, if the effect of multiple risk factors on reoffending is intricate, logistic regression might not provide a complete picture.

Key Takeaways

• Logistic regression helps predict the likelihood of an outcome with two possible results, such as whether someone will reoffend.
• It provides a probability estimate based on various factors.
• It is useful for understanding and predicting binary outcomes related to crime.

Glossary of Key Terms

• Binary Outcome: An outcome with two possible results, such as reoffending or not reoffending.
• Probability: A measure of how likely something is to happen, between 0 (not likely) and 1 (certain).
• Predictor: A factor that helps forecast the outcome, such as previous offenses or age.

Advanced Topics

Interpreting Regression Results

1. Coefficients (Odds Ratios):

   • Each predictor has a coefficient that shows the effect of a one-unit change in that predictor on the odds of the outcome happening.
   • Odds Ratio > 1: Increases the probability of the outcome.

   • Odds Ratio < 1: Decreases the probability of the outcome.

   • Example: If the odds ratio for police presence is 0.7, an increase in police presence is associated with a 30% decrease in the odds of a crime occurring.

2. Predicted Probabilities:

   • The output of logistic regression is a probability that the outcome is “yes” (e.g., a crime will occur).
   • Example: The model might predict a 70% chance that a crime will occur in a given ward based on the inputs.

3. Confusion Matrix:

   • A table that shows how well the model’s predictions match the actual outcomes.
   • Example: It shows how many wards were correctly predicted as high-crime areas versus those incorrectly predicted.

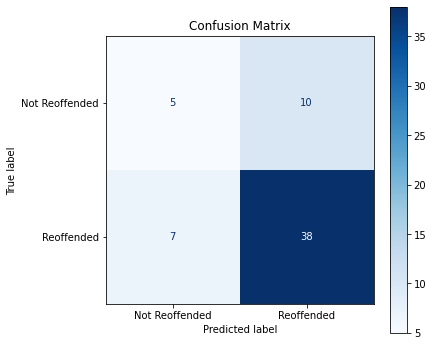   Confusion Matric Showing the Performance of the Logistic Regression Model

Limitations

• Binary Outcomes: Logistic regression is only applicable to outcomes with two categories.
• Linearity: Assumes a linear relationship between factors and the log-odds of the outcome. If the relationship is more complex, logistic regression might not perform well.
• Overfitting: If the model is too complex, it might fit the training data too closely and perform poorly on new data.
• Interpretability: The coefficients represent log-odds, which can be less intuitive to interpret compared to direct probabilities.

Assumptions

• Independence: Assumes that factors are independent of each other.
• Linear Relationship: Assumes that the relationship between predictors and the probability of the outcome is approximately linear in the log-odds scale.

Summary

Logistic regression is a powerful tool for predicting binary outcomes and understanding the impact of various factors on these outcomes. It provides insights that can guide policy decisions and resource allocation. However, it’s important to interpret the results carefully and understand the model’s limitations.